Dans cet article, je vais présenter les simulations de Monte Carlo, expliquer leur pertinence dans trading et décrire une stratégie de trading d’options spécifique que j’ai développée à l’aide de ces simulations. Je partagerai également les résultats des tests rétrospectifs pour illustrer l’efficacité de la stratégie.
1. Que sont les simulations de Monte Carlo ?
Les simulations de Monte Carlo sont une technique informatique utilisée pour modéliser la probabilité de différents résultats dans un processus qui ne peut pas être facilement prédit en raison de la présence de variables aléatoires. Nommées d’après le célèbre casino, ces simulations sont particulièrement utiles en finance car elles permettent d’analyser l’incertitude et les risques.
Le processus implique d’exécuter des milliers ou même des millions de simulations basées sur les mouvements de prix historiques, où chaque simulation projette un résultat futur possible. La distribution qui en résulte fournit aux traders des probabilités de fourchettes de prix sur un horizon temporel donné.
2. Comment les simulations de Monte Carlo sont-elles appliquées au trading ?
En trading, les simulations Monte Carlo permettent d’anticiper comment un instrument financier, tel qu’un ETF comme SPY ou QQQ, pourrait se comporter sur une période future. Le processus examine plusieurs années de données historiques sur les prix et exécute de nombreuses simulations pour projeter les futures distributions de prix. Les résultats montrent généralement une distribution de probabilité des prix futurs, mettant en évidence des mesures clés telles que les intervalles de confiance. Voici un exemple pour SPY :
Ces simulations sont inestimables pour les traders d’options car elles offrent un aperçu de la probabilité qu’une action ou un ETF reste dans les limites de prix supérieures/inférieures sur une période de temps spécifique. Ces informations aident à élaborer des stratégies d’options structurées, comme les Credit Put Spreads, qui profitent lorsqu’un actif reste au-dessus d’un seuil de prix.
3. Exemple de spread de put de crédit
Voici par exemple le résultat de 10 000 simulations réalisées sur SPY pour une prédiction du mouvement dans 15 jours en demandant à l’algorithme de calculer quel pourcentage de données est au dessus du seuil de 565$. Par exemple si l’on considère que cette valeur est un support ou que cette valeur serait le seuil de rentabilité d’une stratégie Credit Put Spread que nous aurions mise en place.
On voit qu’il y a une probabilité de 77% que le ticker soit au-dessus de cette valeur seuil.
Rappelons que les simulations de Monte Carlo observent le comportement passé du ticker sur de nombreuses années, jour après jour, en déduisent une distribution statistique et effectuent des tirs aléatoires orientés comme cette distribution statistique afin de capter le caractère pseudo-aléatoire du marché. Il faudra voir comment ces prédictions se sont réalisées dans le passé.
Notez que pour tenir compte de la distribution historique d’un ticker, nous devons ajuster l’approche de simulation de Monte Carlo dans le code. Plutôt que de supposer une distribution normale des mouvements de prix, je modélise les changements de prix en fonction de la distribution historique réelle des rendements. Cette technique, souvent appelée bootstrapping, échantillonne directement les rendements historiques au lieu de générer des rendements synthétiques basés sur une distribution normale fixe.
C’est alors le genre d’intrigue que nous obtenons :
4. La stratégie : utiliser les simulations de Monte Carlo pour le trading d’options
Utiliser les points morts d’un Iron Condor comme valeurs seuils n’est pas intéressant car les simulations ont montré que les crédits reçus sur la partie Call n’étaient pas suffisants.
Concentrons-nous donc sur la partie Put via les Credit Put Spreads. Pour un ETF donné (nous laisserons de côté les actions en raison des bénéfices), il existe de nombreuses dates d’expiration et de nombreux strikes, chacun avec son propre prix. Quel ETF choisir, quels strikes acheter et vendre et quelles dates d’expiration ?
Pour cela, le programme que j’ai écrit scanne les ETF les plus importants, (“SPY”, “GLD”, “QQQ”, “IWM”, “EEM”), toutes leurs dates d’expiration entre deux nombres de jours (min_days = 30 max_days = 120) et tous les strikes inférieurs au strike OTM pouvant former un Credit Put Spread. Un point est ainsi donné par, par exemple, (SPY, 2024-11-15, put acheté=577$, put vendu=582$).
Pour chaque point, le code effectue ensuite 10 000 simulations Monte Carlo, en regardant 20 ans en arrière et en calculant la probabilité que la clôture du SPY soit supérieure au seuil de rentabilité dans 29 jours (= nombre de jours restants d’ici la date d’expiration). Ensuite, le programme affiche tous les points sous forme d’un graphique avec en abscisse le crédit perçu et en ordonnée la probabilité de Monte Carlo. Seuls les crédits > 0,50 $ et le ratio gain/perte supérieur à 40 % sont sélectionnés.
Le graphique est divisé en 4 quadrants, celui qui nous intéresse le plus est le quadrant nord-est (crédit maximum et probabilité maximale). Le programme détecte alors les deux points qui, dans ce quadrant, ont la probabilité la plus élevée ou le crédit le plus élevé.
Voici un exemple d’affichage :
4. Résultats des backtests
Pour valider cette stratégie, nous avons effectué des backtests en utilisant des données historiques des 15 dernières années. L’idée était de simuler ce qui se serait passé si cette stratégie avait été appliquée dans le passé avec le seuil de rentabilité correspondant à la probabilité calculée au point choisi.
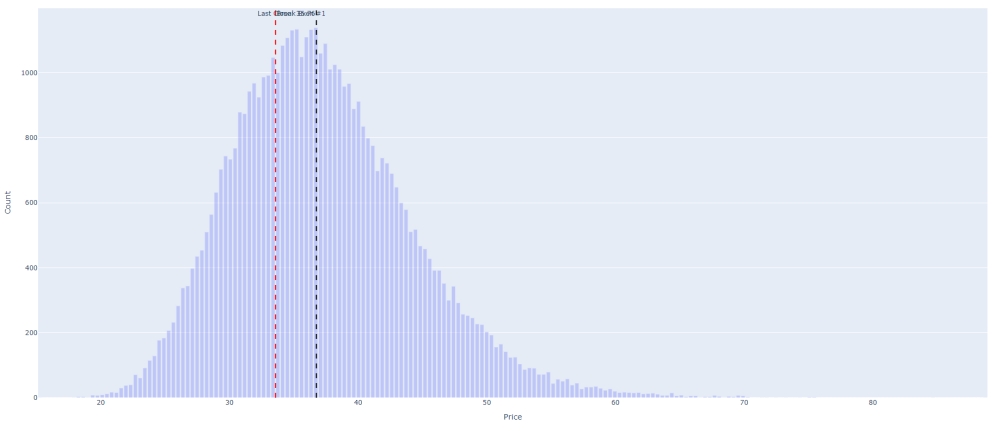
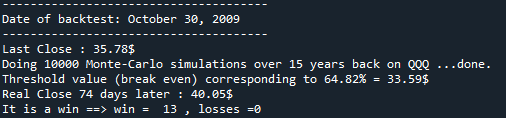
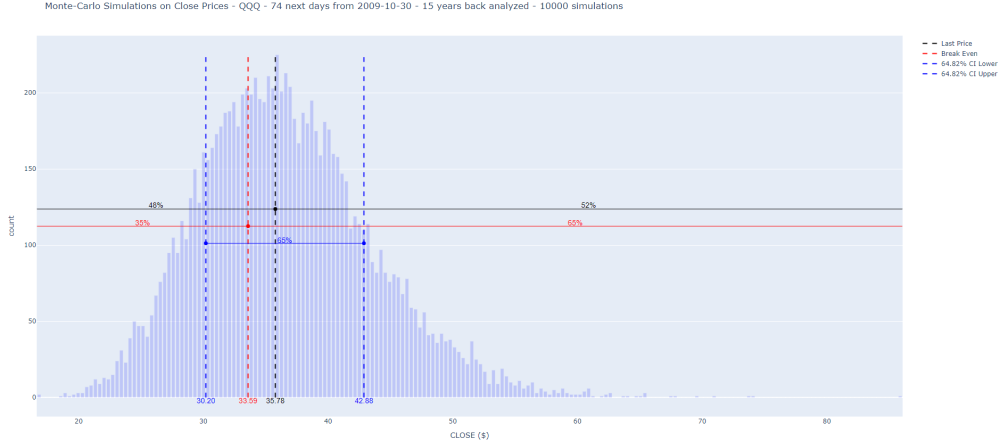
Pour reprendre l’exemple ci-dessus avec le crédit maximum, le backtest répondrait à cette question : pour le ticker QQQ à la date d’expiration du 31/12/2024 (correspondant à 74 jours d’ici, date de rédaction de cet article), le Monte Les simulations de Carlo me disent que la clôture de QQQ a une probabilité de 64,82 % d’être supérieure au seuil de rentabilité de la stratégie. Si j’avais appliqué cette stratégie il y a 15 ans, jour après jour avec le Break Even à cette époque correspondant à ce quantile, la valeur réelle de QQQ aurait-elle effectivement été supérieure à ce Break Even ? Et si oui, combien de fois a-t-il fonctionné entre il y a 15 ans et aujourd’hui, jour après jour ?
Pour être plus précis, lors du backtest, l’algorithme affiche très clairement les résultats des backtests étape par étape :
Exemple de capture d’écran lors du backtest :
et le tracé de l’histogramme pour prouver la cohérence de la valeur seuil :
Cette approche systématique, avec une gestion précise des risques, fournit aux traders un outil puissant pour prendre des décisions éclairées sur la structuration des transactions d’options. Il convient de noter que les performances de chaque stratégie peuvent varier en fonction des conditions du marché. Un backtest cohérent est donc essentiel pour maintenir la stratégie rentable sur des marchés en évolution.
Le résultat final du backtest, pour cette stratégie, est :
Cela signifie que les backtests donnent de meilleurs résultats (taux de victoire de 83,64 %) que les probabilités annoncées par les simulations de Monte Carlo (64,82 %) et que la transaction pourrait être ouverte.
Conclusion
Les simulations de Monte Carlo offrent un moyen scientifique et basé sur des données de projeter les futures fourchettes de prix dans le monde souvent imprévisible du trading. En appliquant ces simulations, nous pouvons développer des stratégies visant à capturer de la valeur en prédisant avec précision les mouvements de prix sur des horizons temporels spécifiques. Les backtests montrent que l’utilisation de cette méthode, en particulier pour les stratégies d’options à long terme comme Iron Condors, peut améliorer considérablement les chances de succès.
Cette approche complète d’autres stratégies d’options et fournit un cadre solide pour structurer des transactions avec une forte probabilité de profit, tout en gérant soigneusement les risques.